 Онлайн калькулятор
Онлайн калькулятор
 Решение матриц
Решение матриц
 Конвертор величин
Конвертор величин
 Решение кв. уравн.
Решение кв. уравн.
 Таблица Брадиса
Таблица Брадиса
 Тригоном. таблицы
Тригоном. таблицы
 Тесты и игры
Тесты и игры
 Решить задачу
Решить задачу
 Таблица производных
Таблица производных
 Калькулятор дробей
Калькулятор дробей
 Фонетический разбор
Фонетический разбор
 Редактор формул
Редактор формул
Теорема Ролля
Если дана непрерывная функция f(х) на участке а, b и внутри этого участка, она. в каждой точке имеет производную, а значение f(a)=f(b). Значит внутри участка есть значение х=с, от него производная приравнивается к нулю f(c)=0.
f(x) непрерывная функция достигает на участке наименьшее значение m и наибольшее значение M. Если m =M это означает что, данная функция на всем участке имеет одни и те же значения. Мы знаем что производная от постоянной приравнивается к нулю, значит при m=M. производная внутри участка равняется нулю. Исходя из того что m - наименьшее значение, а М - наибольшее, можно считать что m<М. Предположим что обозначение М отлично от общего значения на концах отрезка и наибольшее значение она достигнет внутри участка. Точкой этого значения будет х=с. Следовательно f(c)=0 и доказало теорему Ролля.
Иногда эта теорема излагается иначе: в функции между двух корней имеется хотя бы один корень первой производной f(a)=f(b)=0.
Другими словами, если дано условием f(a)= f(b), то ординаты кривой y=f(x) которые соответствуют концам участка - равные, и внутри данного участка есть производная. Значит у кривой есть касательная. Данная теорема доказывает что, в этом случае внутри участка есть хотя бы одна точка, в которой производная приравнивается к нулю.
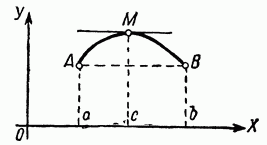
Однако когда условие о существовании производной f(x) во всех точках внутри участка по данной теореме не выполняется, она может быть неверной.
к примеру
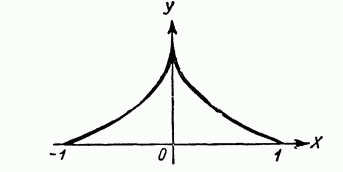
непрерывна в участке
но производная f(x) = - 2/(3?x), внутри промежутка в нуль не превращается. Так получается из-за того что f(х) не существует и превращается в бесконечность при х=0.
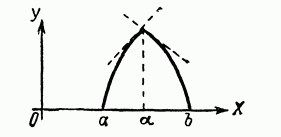
Разберем еще один пример. Есть кривая y=f(x) у которой f(a)=f(b)=0. На чертеже видим касательная находится внутри участка а,b. К оси ОХ не параллельна, значит в нуль не превращается. Так получается из-за того, что у кривой в точке х=а есть две разные касательные с двух сторон, а значит производной у нее нет. По данной теореме условие не выполнено.
Разберем одну задачу: Нужно доказать , что функция f(х)=х2-3х+2 не противоречит условию данной теоремы, на участке (1,2) и найти точку с ?(1,2) в которой f(c)=0.
Данная функция f(х)=х2-3х+2 дифференцируема на участке (1,2) и, на его концах принимает обозначение:
f(1) = f(2) = 0.
Тогда по теореме Ролля, есть точка с ?(1,2), в которой f(c)=0.
Находим производную функции f(x) = 2x-3. Находим значение в точке с . Полученное приравняем к нулю
f (x) = 2c-3, следовательно, с = 3/2
Наш ответ с = 3/2
Широкий выбор качественной продукции от немецкого производителя, имеющий индивидуальные преимущества. Узнайте какие, перейдя по ссылке окна рехау в самаре (http://oknaforever.ru/produktsiya)
- Блог пользователя kak-reshit
- Войдите на сайт для отправки комментариев


 Образовательный портал
Образовательный портал Reshit.ru может исчезнуть — нужна ваша поддержка!
Reshit.ru может исчезнуть — нужна ваша поддержка!
Вроде бы все понятно, но вот в последней задаче я совершенно запутался. Если можно, разместите пожалуйста как можно больше примеров с использованием этой теоремы.
Вот объясните мне как может непрерывная функция достигать наименьшее и наибольшее значение?!
Мне очень повезло, приведенная задача как раз одна из тех, что у меня в билетах на экзамен. А другие похожие, только числа другие. Спасибо, хоть с этим разберусь)))