Асимптота

Асимптота в переводе с греческого языка обозначает - не совпадающая. То есть это несколько продолженная линия, которая в приближении к кривой или какой-либо её части, делает так, что бы расстояние у них было меньше чем у всех данных величин. Другими словами D соприкасается с кривой, на не кончающемся участке оси координат. И любая линия которая параллельна D, дублирующая её, не сможет быть с тем же названием, потому что по произволению расстояние между ней и кривой не может идти в меньшую сторону. Из чего следует что D имеет ограниченные рамки относительно кривой. Когда в Греции ученые математики изучали какими свойствами обладает кривая линия в конусе по пересечению его плоскости, они вывели если ветви гиперболы несколько удлиненны, то обязательно приблизятся к прямым идущим от центра фигуры при этом равно наклонены к оси фигуры. Данные прямые и есть D. Ньютон доказал что кривые алгебраические D, идут они от последнего третьего порядка. Следовательно, есть как прямые (Асимп.) так и кривые (Асимптотическая кривая) D линии.
Отталкиваясь от всего выше сказанного, найдем уравнение D. y=f(х) - уравнение кривой, координаты х,у - касательная в точке = Y - y =dy/dx(X-x) либо У =(dy/dx) X+y-x(dy/dx).

Для перехода к D нужно любое из предположений:

- х и у = + или - бесконечность.
- х = + или - бесконечность, у = крайнему числу.
- у = + бесконечность, х = крайнему числу.

Потому как данные предложения показывают что расстояние из начала координат до точки касания, бесконечно.

Если Вам нужен проект на газоснабжение. Перейдите по ссылке http://proekt-gaz.ru/forum/ , где вы сможете заказать готовый проект.

Асимптота бывает нескольких видов - вертикальная, горизонтальная и наклонная.

Вертикальная - это прямая линия типа х=а и с условием что существует придел lim(х от а) f(x) = ?. находить нужно два односторонних предела, для того что бы знать поведение функции с двух сторон.

Горизонтальная - так же прямая линия типа y=a с условием что существует предел lim (x от + или - ?) f(x) =a

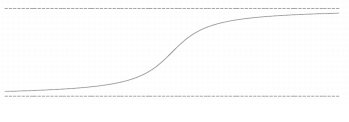
Наклонная - тип у=kх + b с пределами: lim(x от +,- ?) f(x) / x = k, и lim (x от +,- ?) (f(x) - kx) = b. В данной функции не больше двух наклонных асимптот.

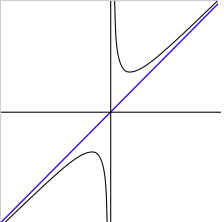
Существует связь наклонной и горизонтальной асимптот, она заключается в вычислении предела lim (x +,- ?) f(x)/x =0, значит они совпадают.

Частный случай горизонтальной асимптоты является
lim (x +,- ?)f(x)/x =0, следовательно,

- функция имеет только горизонтальную асимптоту когда х зависит от + бесконечности, так же и при х зависящем от - бесконечности. Асимптот может и не быть.
- существующие асимптоты зависят от существования пределов.

Рассмотрим на примере:

найти асимптоту с помощью выделения целой части
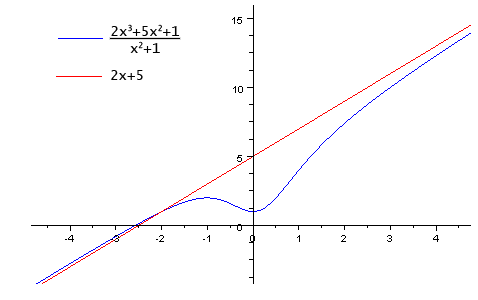
f(X) = 2x³+5x²+1/x²+1
поделив данное равенство получаем
f(X) = 2x + 5 +(-2x-4 / x²+1) = 2x + 5 + (-2) (x+2/x²+1)
x от ?, х+2/х²+1 от 0. или
Ответ: lim (x от +, - ?) f(x) = lim (x от +,- ?) (2x+5) = +,- ?. и у= 2х + 5.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---