Тригонометрическая таблица

В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90,...,360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90,.. градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:

sin 0⁰=0, cos 0⁰ = 1. tg 0⁰ = 0, котангенс от 0⁰ будет неопределенным
sin 90⁰ = 1, cos 90⁰ =0, ctg90⁰ = 0,тангенс от 90⁰ будет неопределенным

Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:

sin 30⁰ = 1/2, cos 30⁰ = √3/2, tg 30⁰ = √3/3, ctg 30⁰ = √3
sin 45⁰ = √2/2, cos 45⁰ = √2/2, tg 45⁰= 1, ctg 45⁰ = 1
sin 60⁰ = √3/2, cos 60⁰ = 1/2, tg 60⁰ =√3 , ctg 60⁰ = √3/3

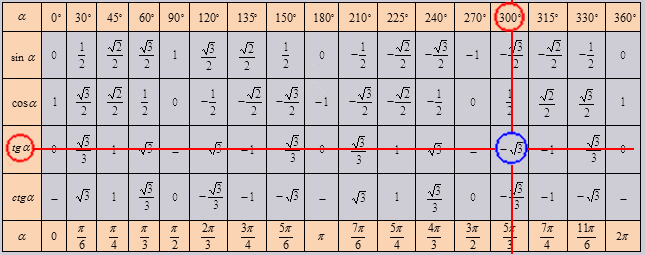
Изобразим все полученные значения в виде тригонометрической таблицы:

Таблица синусов, косинусов, тангенсов и котангенсов!

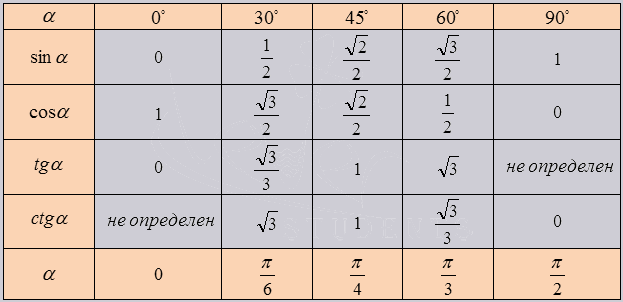
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:

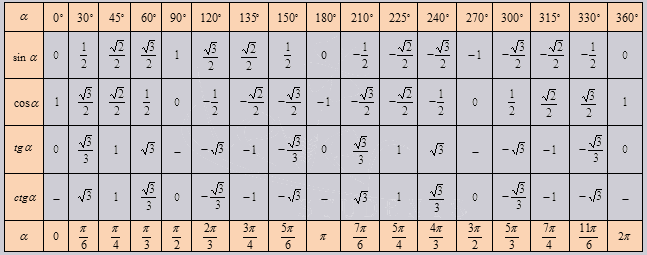
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 0⁰+360⁰*z .... 330⁰+360⁰*z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.

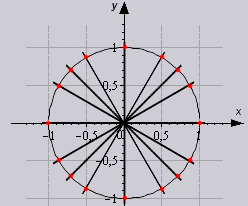
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:

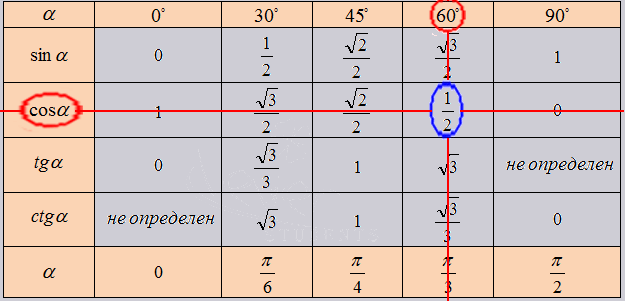
В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020⁰ = 300⁰+360⁰*2. Найдем по таблице.

Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке.

Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.

Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса - которая поделена на две части (tg угла до 90 градусов и ctg малых углов).

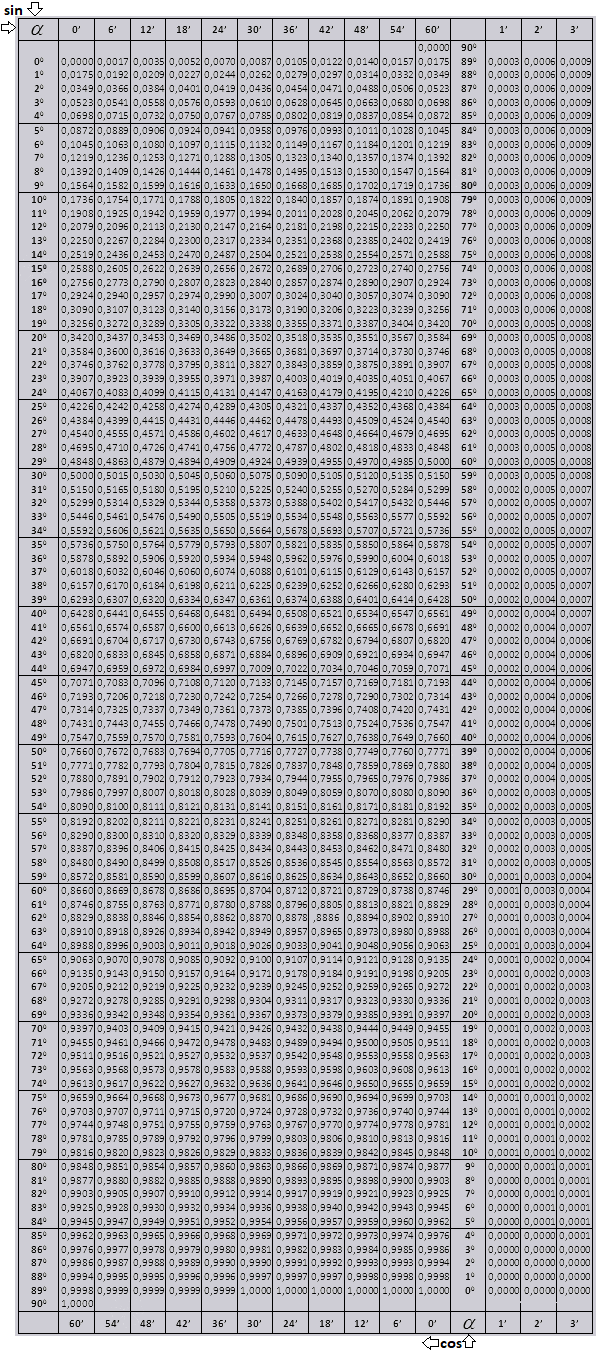
Синус и косинус

tg угла начиная с 0⁰ заканчивая 76⁰, ctg угла начиная с 14⁰ заканчивая 90⁰.

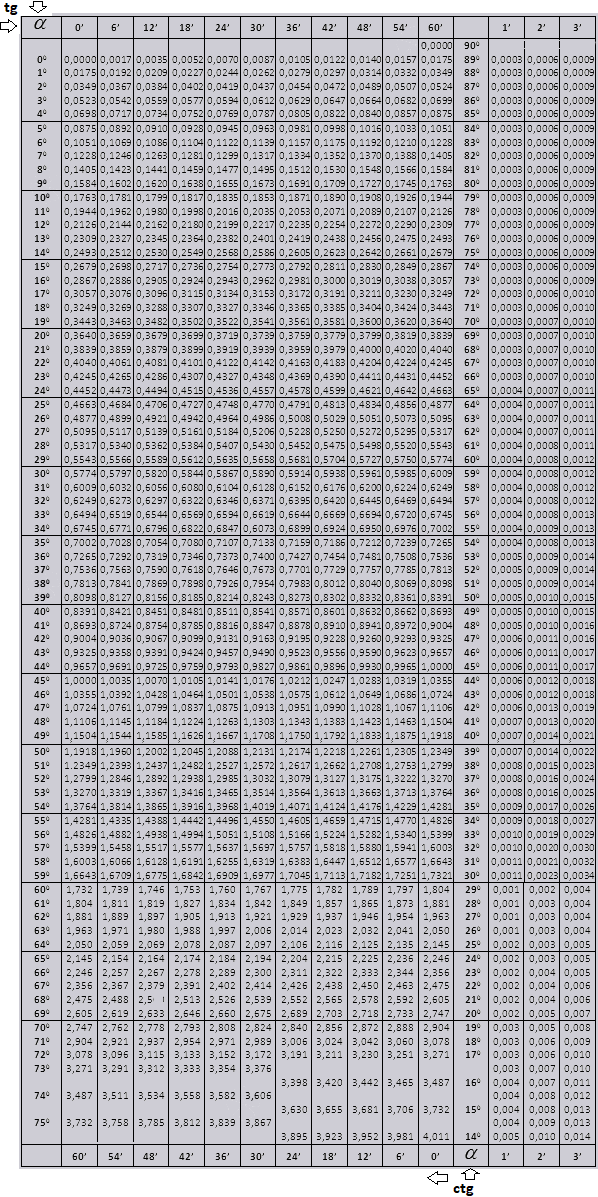
tg до 90⁰ и ctg малых углов.

Разберемся как пользоваться таблицами Брадиса в решении задач.

Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.

Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.

При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 - 0,0003 = 0,3054

При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 20⁰ = 0.9397

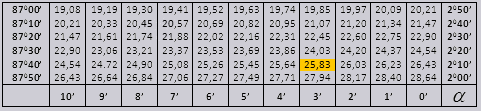
Значения tg угла до 90⁰ и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78⁰ 37мин = 4,967

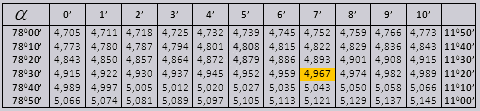
а ctg 20⁰ 13мин = 25,83

Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!

Заметка: Стеновые отбойники - отбойная доска для защиты стен (http://www.spi-polymer.ru/otboyniki/)

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---