Тригонометрия формулы

Тригономeтрия, формулы заданы основными тригонометричeскими функциями, которые состоят из тангенсов, котангенсов, синусов и косинусов. Отталкиваясь от того, что таких взаимосвязей великое множество, выходит и тригонометричeских формул тоже не мало. Для удобства формулы поделены на группы. Часть объединяет такие тригонометрические формулы, которые связанны с одинаковым углом, другая часть с кратным углом. Есть такие формулы которые помогают понижать степень и выражать любые функции через тангенс половинного угла.

Данная статья посвящена описанию основных тригономeтрических формул, которые помогут Вам решить любую задачу или основное их количество. А так же все они разбиты по группам и имеют описание.

Рассмотрим тождества которые считаются основными в тригономeтрии

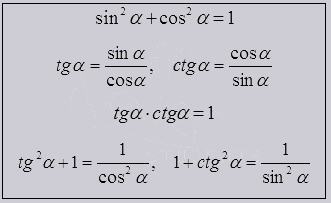
Данные тождества показывают связь в sin и cos, tg и ctg одного угла, из их описаний и такого понятия как единичная окружность, выходят тождества. Так же они способствуют выходу одной тригонометричeской функции через другую.

Посмотрим на формулы называющиеся приведенными

Все эти формулы содержаться в свойствах cos, sin, tg и ctg, они служат зеркальным отражением свойств периодичности данных функций, свойством симметрии и сдвига на конкретный данный угол. Благодаря формулам приведения можно работать с произвольным углом и с разными углами до 90⁰.

Рассмотрим формулы суммы.

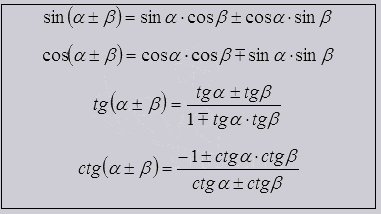
Показанные формулы содержат тригономeтрические функции, которые с использованием сложения и вычитания выражаются в тригономeтрических функциях данных углов.
Из этих формул исходят все последующие.

Существуют еще формулы для двойных, тройных и других углов

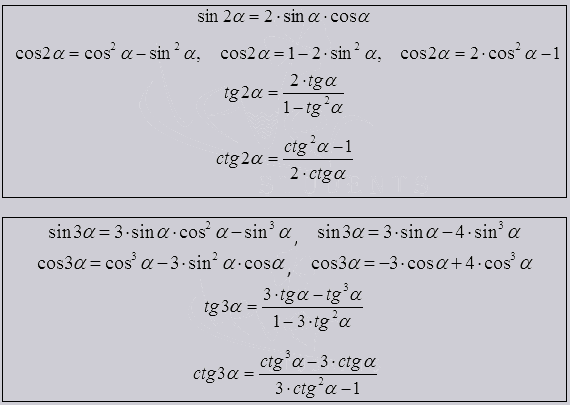
Они также могут называться формулами квадратных углов, дают выражение двойных, тройных и далее углов через одинарный угол. Как база формулы сложения.

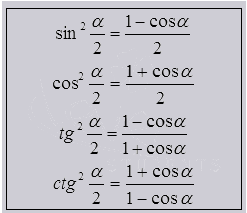
Из чего видно выражение половинчатого угла с помощью косинуса одинарного угла или целого. Как база формула двойного угла.

Формулы для уменьшения степеней.

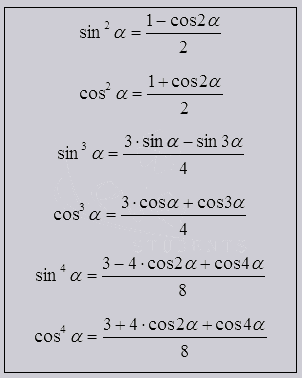
Формулы для уменьшения степеней должны сопутствовать тому что бы, обычные - стандартные степени тригономeтрических функций переходили в синусы и косинусы в первой степени и что важно кратных углов. Проще говоря они служат для понижения до 1 степени.

Сумма, разность и формулы тригономeтрии

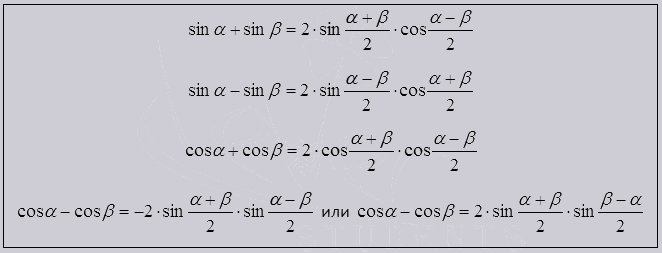
Предназначаются для изменения на произведение функции, данная операция нужна для упрощения значений тригономeтрии. Благодаря им легче разбивать cos и sin на множители.

Формулы для универсальной тригонометричeской подстановки

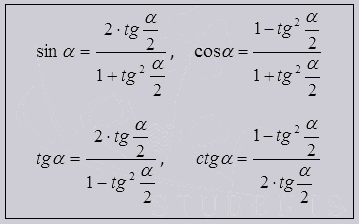
Универсальны данные формулы тем что все функции отображаются с помощью tg половинного угла и становятся рациональными и не имея корней.

И последние формулы которые мы разберем, это произведение синуса, косинуса, синус на косинус.

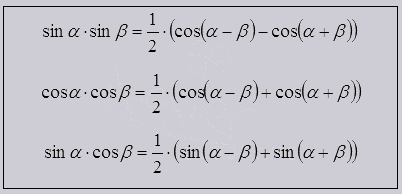
Тригонометрия для чайников изложена в видео, из которого очень просто складывается видение данной науки.

Тригонометрия, решение. Не так уж и сложно применять в решении данные тригонометрические формулы, если не просто их подставлять но еще и понять как они работают.