 Онлайн калькулятор
Онлайн калькулятор
 Решение матриц
Решение матриц
 Конвертор величин
Конвертор величин
 Решение кв. уравн.
Решение кв. уравн.
 Таблица Брадиса
Таблица Брадиса
 Тригоном. таблицы
Тригоном. таблицы
 Тесты и игры
Тесты и игры
 Решить задачу
Решить задачу
 Таблица производных
Таблица производных
 Калькулятор дробей
Калькулятор дробей
 Фонетический разбор
Фонетический разбор
 Редактор формул
Редактор формул
Формулы сокращенного умножения
Для того что бы упростить алгебраические многочлены, существуют формулы сокращенного умножения. Их не так уж и много и они легко запоминаются, а запомнить их нужно. Обозначения которые используются в формулах, могут принимать любой вид (число или многочлен).
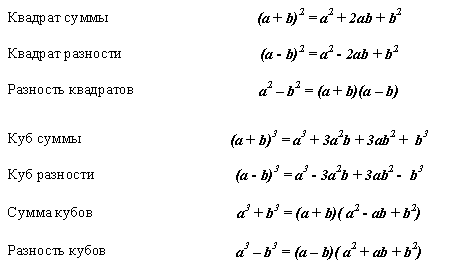
Первая формула сокращенного умножения называется разность квадратов. Она заключается в том что из квадрата одного числа отнимается квадрат второго числа равен величине разности данных чисел, а также их произведению.
а2 - b2 = (а - b)(a + b)
Разберем для наглядности:
222 - 42 = (22-4)(22+4)=18 * 26 = 468
9а2 - 4b2c2 = (3a - 2bc)(3a + 2bc)
Вторая формула о сумме квадратов. Звучит она как, сумма двух величин в квадрате равняется квадрату первой величины к ней прибавляется двойное произведение первой величины умноженное на вторую, к ним прибавляется квадрат второй величины.
Благодаря данной формуле, становится намного проще вычислять квадрат от большого числа, без использования вычислительной техники.
Так к примеру: квадрат от 112 будет равен
1) В начале разберем 112 на числа квадраты которых нам знакомы
112 = 100 + 12
2) Вписываем полученное в скобки возведенные в квадрат
1122 = (100+12)2
3) Применяя формулу, получаем:
Третья формула это квадрат разности. Которая гласит о том, что две вычитаемые друг друга величины в квадрате равняются, тому что, от первой величины в квадрате отнимаем двойное произведение первой величины умноженное на вторую, прибавляя к ним квадрат второй величины.
(а +b)2 = а2 - 2аb + b2
где (а - b)2 равняется (b - а)2. В доказательство чему, (а-b)2 = а2-2аb+b2 = b2-2аb + а2 = (b-а)2
Четвертая формула сокращенного умножения называется куб суммы. Которая звучит как: две слагаемые величины в кубе равны кубу 1 величины прибавляется тройное произведение 1 величины в квадрате умноженное на 2-ую величину, к ним прибавляется тройное произведение 1 величины умноженной на квадрат 2 величины, плюс вторая величина в кубе.
Пятая, как вы уже поняли называется куб разности. Которая находит разности между величинами, как от первого обозначения в кубе отнимаем тройное произведение первого обозначения в квадрате умноженное на второе, к ним прибавляется тройное произведение первого обозначения умноженной на квадрат второго обозначения, минус второе обозначение в кубе.
(а-b)3 = а3 - 3а2b + 3аb2 - b3
Шестая называется - сумма кубов. Сумма кубов равняется произведению двух слагаемых величин, умноженных на неполный квадрат разности, так как в середине нет удвоенного значения.
а3 + b3 = (а+b)(а2-аb+b2)
По другому можно сказать сумму кубов можно назвать произведение в двух скобках.
Седьмая и заключительная, называется разность кубов (ее легко перепутать с формулой куба разности, но это разные вещи). Разность кубов равняется произведению от разности двух величин, умноженных на неполный квадрат суммы, так как в середине нет удвоенного значения.
а3 - b3 = (а-b)(а2+аb+b2)
И так формул сокращенного умножения всего 7, они похожи друг на друга и легко запоминаются, единственно важно не путаться в знаках. Они так же рассчитаны на то, что их можно использовать в обратном порядке и в учебниках собрано довольно много таких заданий. Будьте внимательны и все у вас получится.
Если у вас появились вопросы по формулам, обязательно пишите их в комментариях. Будем рады ответить вам!
Если Вы находитесь в декретном отпуске, но хотите зарабатывать деньги. Просто перейдите по ссылке . Там все очень подробно написано и показано. Будет интересно!
- Блог пользователя kak-reshit
- Войдите на сайт для отправки комментариев


 Образовательный портал
Образовательный портал Reshit.ru может исчезнуть — нужна ваша поддержка!
Reshit.ru может исчезнуть — нужна ваша поддержка!
Не путаться в знаках получается с трудом конечно, но наш преподаватель это уже понял и не сильно мне бал снижает. Видно, что формулу помню, а знаки путаю. Вместо тройки четыре иногда ставит.
Эти формулы очень простые, вы видно мало ними пользуетесь. Я их даже не учила, просто на практике запомнились, теперь даже не нужны а помню все равно)))
Согласен с Линейкой на все сто. Даже я запомнил, хотя у меня память ужасная!
Я себе эти формулы сокращенного умножения на всех тетрадках и учебниках писал, и только когда они уже были не нужны понял что наконец их наизусть выучил.