 Онлайн калькулятор
Онлайн калькулятор
 Решение матриц
Решение матриц
 Конвертор величин
Конвертор величин
 Решение кв. уравн.
Решение кв. уравн.
 Таблица Брадиса
Таблица Брадиса
 Тригоном. таблицы
Тригоном. таблицы
 Тесты и игры
Тесты и игры
 Решить задачу
Решить задачу
 Таблица производных
Таблица производных
 Калькулятор дробей
Калькулятор дробей
 Фонетический разбор
Фонетический разбор
 Редактор формул
Редактор формул
Формулы производных
Что такое производная функция - это основное математическое понятие, находится на одном уровне с интегралами, при анализе. Данная функция в определенной точке дает характеристику скорости изменений функции в данной точке.
Такие понятия как дифференцирование и интегрирование, первое расшифровывается как действие поиска производной, второе наоборот, восстанавливает функцию отталкиваясь от данной производной.
Вычислениям производной отводится важная часть в дифференциальных расчетах.
Для наглядного примера, изобразим производную на координатной плоскости.
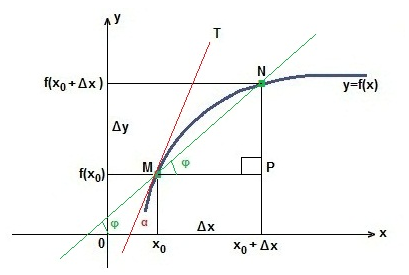
в функции у=f(х) фиксируем точки М в которой (х0; f(X0)) и N f (x0+?x) к каждой абсциссе есть приращение в виде ?x. Приращением называется процесс когда изменяется абсцисса, тогда меняется и ордината. Обозначается как ?у.
Найдем тангенс угла в треугольнике MPN используя для этого точки М и N.
tg? = NP/MP = ?у/?x.
При ?x идущем к 0. Пересекающая МN все ближе к касательной МТ и угол ? будет ?. Следовательно, tg ? максимальное значение для tg ?.
tg ? = lim от ?x-0 tg ? = lim от ?x-0 ?у/?x
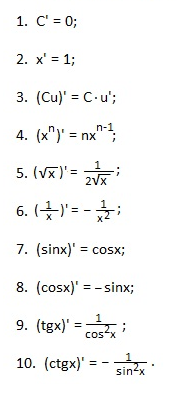
Если проговаривать формулировку каждой формулы производных. Таблица будет проще запоминаться.
1) Производная от постоянного значения равняется 0.
2) Х со штрихом равняется единице.
3) Если есть постоянный множитель, просто выносим ео за производную.
4) Чтобы найти производную степень, нужно показатель данной степени умножить на степень с таким же основанием, у которого показатель на 1 меньше.
5) Поиск корня равен одному, деленному 2 этих корня.
7) П синус равняется косинусу
8) П косинус равняется синусу со знаком минус.
9) П тангенс равняется одному, деленному на косинус в квадрате.
10) П котангенс равняется одному со знаком минус, деленная на синус в квадрате.
В дифференцировании также существуют правила, которые тоже проще выучить проговаривая их в слух.
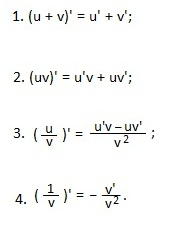
1) Очень просто, п. слагаемых равняется их сумме.
2) Производная в умножении равняется умножению первого значения на второе, прибавляя к себе умножение второго значения на первое.
3) Производная в делении равняется умножению первого значения на второе, отнимая от себя умножение второго значения на первое. Дробь деления на второе значение в квадрате.
4) Формулировка является частным случаем третьей формулы.
- Блог пользователя kak-reshit
- Войдите на сайт для отправки комментариев


 Образовательный портал
Образовательный портал Reshit.ru может исчезнуть — нужна ваша поддержка!
Reshit.ru может исчезнуть — нужна ваша поддержка!
Вот когда на координатной плоскости изображают формулу производной все становится понятно, а у нас преподаватель просто все на словах, сидим как бараны, даже не догадываемся о чем речь то идет. Спасибо вам!
Помню как не хотелось учить эту таблицу производных. Хотя зная ее на память очень даже полезно, на годовом модуле мне пригодились))))))
Помню как не хотелось учить эту таблицу производных. Хотя зная ее на память очень даже полезно, на годовом модуле мне пригодились))))))
Вот как можно вообще эти правила выучить вслух проговаривая?!
Ну не знаю почему вы утверждаете что на одном уровне с интегралами, а получается что интегралы в сто раз сложнее решать чем иметь дело с производными.