Таблица Брадиса: тангенсы, котангенсы, синусы и косинусы с инструкцией.

Как бы не совершенствовалась вычислительная техника, определение синусов, косинусов, тангенсов и котангенсов с помощью таблицы Брадиса будет всегда актуально.
Таблица Брадиса создана выдающимся педагогом-математиком Владимиром Модестовичем Брадисом. Чтобы вы научились пользоваться таблицами Брадиса, которые представлены ниже, рекомендуем сначала прочесть инструкцию.

Таблица брадиса - инструкция

1. Возьмите саму таблицу Брадиса. Если у вас нет её в напечатанной виде, то воспользуйтесь нашими таблицами брадиса. Откройте соответствующую главу: тангенсы-котангенсы или синусы-косинусы. Для примера возьмем синус.



2. Убедитесь, какой угол нужен Вам для решения задачи. Таблицу Брадиса можно и без проблем применить в том разе, даже когда угол является дробным, то есть его расчет происходит в градусах и минутах. Если величина угла подаётся в радианах, преобразуйте её значения в градусы. Оно будет равняться произведению размера ( считают в радианах) , помноженному на отношение 180-ти градусов на значение π и подаётся общей формулой, а именно : α_град=α_рад*180°/π, при этом — α_град величина нужного угла (подаётся в градусах), α_рад — величина, которая подаётся в радианах.
3. В таблице Брадиса, Вам будут видны некие рядки, которые будут находиться и по горизонтали, и по вертикали. Обратите внимание на самый крайний ряд, находящийся слева. Вверху левого угла находится слово sin, а под ним расположился столбец из цифр с наименованием градуса. Это целая величина градусов. Отыщите число, которое будет напрямую соответствовать величине целых градусов в уже заданном Вами угле. К примеру, вам дан в задании угол равный 27°18'. Обратите внимание, что в крайнем левом столбце имеется число 27. Потом в самой верхней строчку отыщите число 18. На перекрёстке строчки и столбика Вы сможете увидеть нужное для Вас значение.
4. Сделайте акцент на то, что градусы в таблице Брадиса идут между собой подряд, а минуты чередуются через шесть. К примеру, 18 минут в таблице подаваться будут, а 19 найти Вы уже не сможете . Чтобы высчитать синус нужного угла, величину минут которого непосредственно не будет кратно 6ти, применяются некие поправки. Они расположились в правой части таблицы. Посчитайте разницу между количеством заданных минут в нужном угле и самом ближайшем угле, где величина минут будет кратна 6ти. Если это различие будет составлять приблизительно 1, 2, 3 минуты, то Вы просто добавьте требуемое значение к конечной цифре величины синуса самого малого угла. Если разность будит близиться к 4 или 5, возьмите величину самого близкого большого угла и вычтите от конечного числа величину первой или второй поправки.

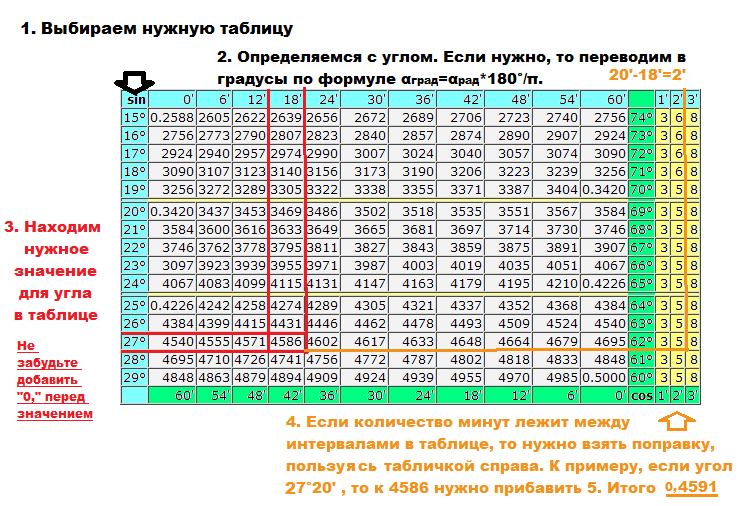
Таблица Брадиса: Косинусы-синусы

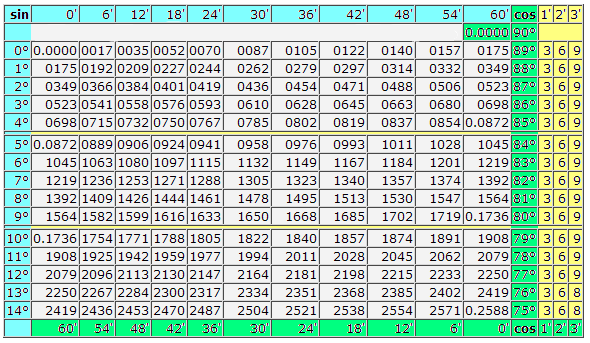
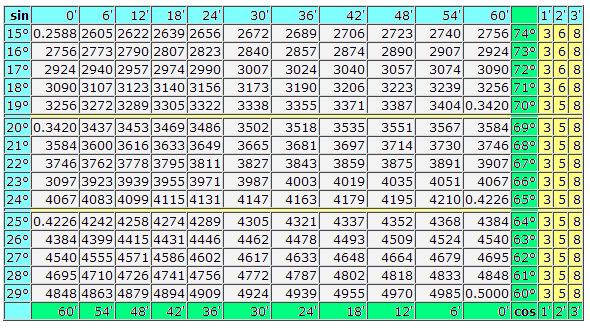
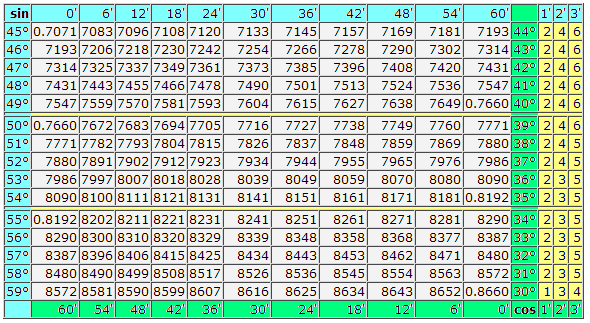
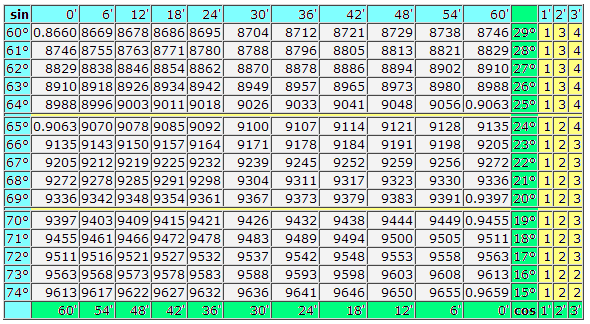
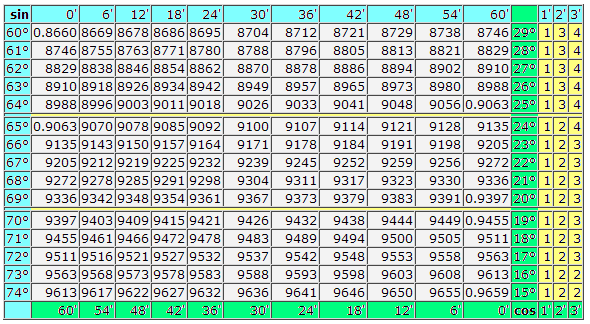
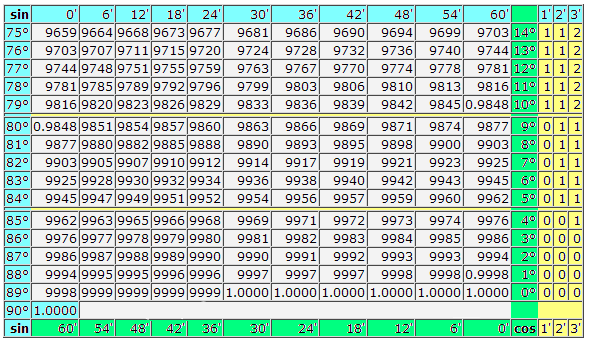
Таблица Брадиса: тангенсы - котангенсы

tg и ctg больших углов

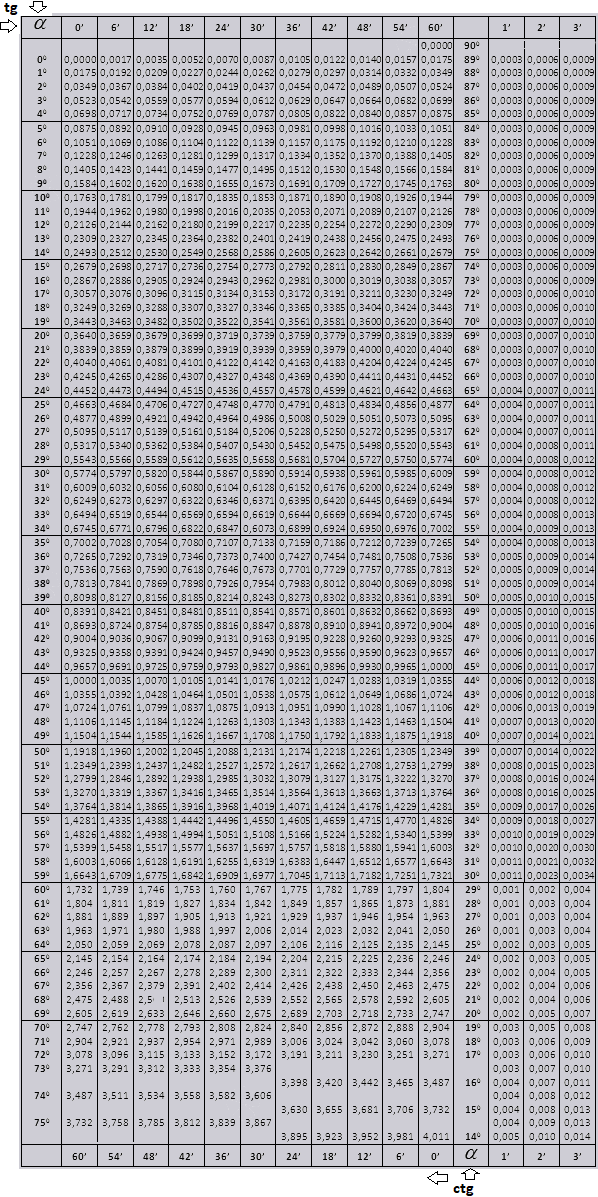
tg и ctg малых углов

Если по пользованию таблицами Брадиса у вас возникли какие то вопросы, то пишите их в комментариях.
Спасибо за пользование нашим сервисом.

Москвичей возможно заинтересует - дистанционное образование в москве. Учиться дистанционно - шикарная возможность стать свободнее уже сейчас.