Формулы тригонометрии

Взаимосвязь основных тригонометрических функций, каких как косинус и синус, тангенс и котангенс - называется формулы тригонометрии. Из-за того что взаимосвязей очень большое количество, соответственно и формул не меньше. Часть формул объединяет тригонометрические функции в зависимости от угла, который может быть либо кратным, либо одинаковым. Так же может выражаться от тангенса половинного угла. Так же через понижение степени.
Мы разберем самые основные из тригонометрических формул. С помощью которых можно решить большинство тригонометрических заданий. Для большего удобства объединим их по значению, по таблицам.

Начнем с тригонометрических тождеств.

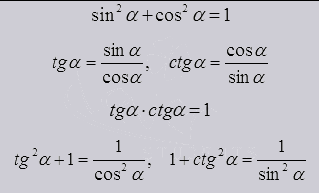
Основы в тригонометрических тождествах определяют взаимосвязь косинуса и синуса, тангенса и котангенса в одном угле. И выходят из их определения и единичной окружности. Дают возможность выделить через любую функцию другую.

Далее рассмотрим тригонометрические формулы приведения.

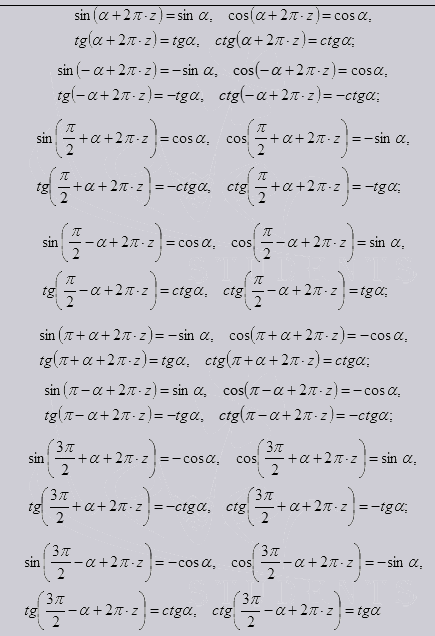
Они вытекают из свойств синусов, косинусов, котангенсов и тангенсов. Тем самым выражают такие свойства функции как: периодичность, симметричность и сдвиг к рассматриваемому углу. так же дают возможность работать с углами в радиусе до 90 градусов и произвольные углы.

Формулы на сложение.

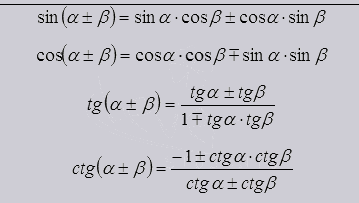
Из данных формул видно что функции на сумму или разность от 2 углов выводятся из их же тригонометрических функций. Так же являются основой для формул двойных, тройных и других углов.

Формула для двойных, тройных и других углов.

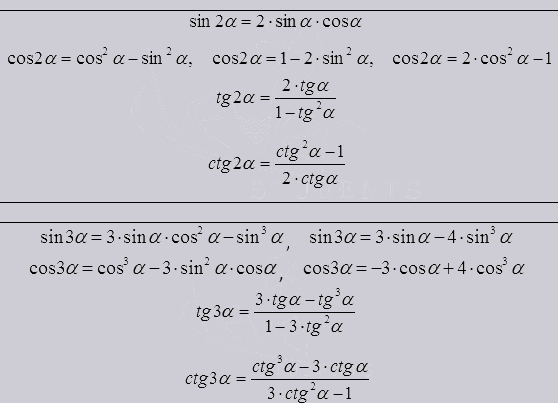
Из них видно что тригонометрическая функция двойного, тройного или какого то ни было угла выводится из т.ф. одинарных углов.

Так же как и одинарные, двойные, тройные и т.д. существуют и половинные углы

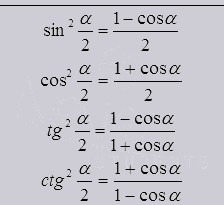
Из формул половинного угла видно, что он выходит из косинуса угла целого.

Так же существуют методы понижения степени выглядят они как:

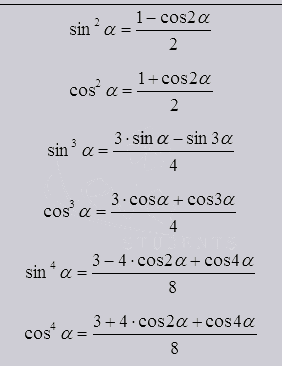
С помощью их использования возможно понизить функцию до первой степени. Взаимодействуя с натуральными степенями функций переводить до синусов и косинусов только кратных углов, в первую степень.

Сумма и разность в тригонометрической функции.

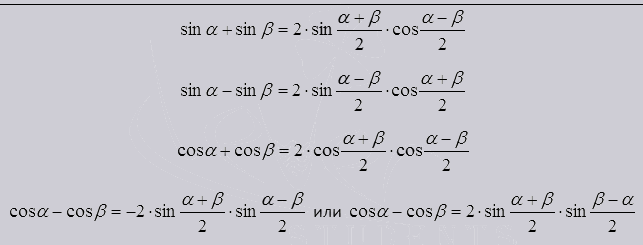
Помогают упростить тригонометрическое выражение, и разложить на множители синусы и косинусы.

Произведение синуса, косинуса, и одно на другое.


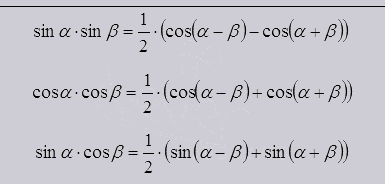
Метод универсальной тригонометрической подстановки.

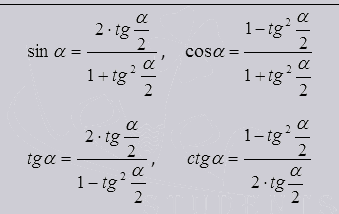
Такая подстановка удобна тем, что функции получаются без корней.

Заметка: Актуальные предложения, участие в тендерах на строительство бесплатное! Перейдите по ссылке строительно монтажные тендеры (http://www.b2bsearch.ru/tenders/stroy) узнайте подробнее.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---