Формула площади трапеции

В статье понятно и доступно разберем формулу площади трапеции, но для начала отработаем основные понятия!
Трапеция это геометрическая четырехугольная фигура, состоящая из двух параллельных линий называющихся основанием и двух боковых линии не являющиеся параллельными, называющиеся боковые стороны. Линия которая соединяет стороны как основные так и боковые посередине, называется - средней линией, высота выводится под углом 90⁰.
Площадью трапеции называется участок на плоскости, который ограничен данной фигурой, обозначается в единицах квадратных.

В случае если мы знаем величину средней линии k, формула меняется на более легкую, она приравнивается к половине суммы длины основных линий

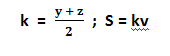
В случае когда мы знаем длину всех сторон, можно рассчитать площадь используя данную формулу

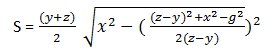
Если разобрать данную формулу на примере, то мы получим следующее:
Рассмотрим для ясности: трапеция с длиной боковых линий х = 5 см, g = 4 см, основные линии y = 3 см, z = 7 см. Требуется найти S = ?.

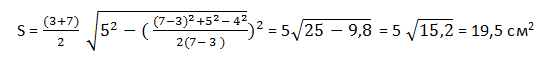
Трапеция бывает однобокой, ещё ее называют равнобедренной - так как диагонали равны между собой. Для нее формула может складываться через радиус вписанной в нее окружности, диагонали и углы прилегающие к основанию.
В случае когда мы знаем длину диагоналей и угол находящийся между ними:

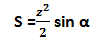
В том случае когда выводим формулу с помощью боковых сторон и углов прилегающих к основанию. Формула будет выглядеть так:

S = x * sin ?(y - x * cos ?)
S = x * sin ?(z + x * cos ?)

Вывод: Если нам известно одно основание из двух и величины углов принадлежащие этому основанию, мы без труда сможем узнать площадь трапеции.

Трапеция бывает криволинейной - это тогда, когда трапеция находится на оси координат, ограничена графиком продолжительной функции.

В случае когда основание трапеции находится на оси х и ограничено точками x1 = z, x2 = y. Вычислить площадь трапеции помогут интегралы


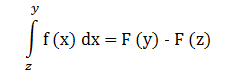
где F (z) - значение в точке z
F (y) - значение в точке y

Разберем для наглядности: Криволинейная трапеция, ограниченная функцией y = f(x). Функция F(x) = - x3 - 27x2 - 240x - 8. Нужно найти S = ?. Фигура ограничивается: графиком сверху y = f(x)., снизу ОХ осью, слева х = (-10), справа х = (-8).
Пользуемся данной формулой, получаем:

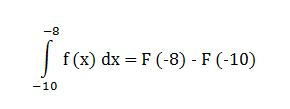
В условиях задачи дана функция. С помощью нее найдем значения точек.
1) F(-8) = -(-8)3 - 27 х (-8)2 - 240 х (-8) - 8 = 24-1728+1920 - 8 = 696
2) F(-10) = -(-10)3 - 27 х (-10)2 - 240 х (-10) - 8 = 1000-2700+240 - 8 = 692
3) F(-8) - F (-10) = 696 - 692 = 4
Ответ: S = 4

Вот собственно и всё по формулам площади для разных видов трапеций. Если у вас появились какие то вопросы, обязательно пишите их в комментариях. Успехов в учебе.
vamsochinenie.ru - база сочинений на самые разные темы.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---