Геометрический смысл определенного интеграла

Геометрия способна помочь решать различные задачи, в том числе относительно вычисления площади, то, что является неотъемлемой частью теории площади. Достаточно легко и просто рассчитать площадь, когда она является легко распознаваемой и с виду представляет собой какую-ту известную геометрическую фигуру правильной формы. Совсем другое, когда речь о вычислении площади неправильных фигур и тогда на помощь можно позвать другие хитрости геометрии, в том числе использовать геометрический смысл определенного интеграла.

Интегральное вычисление позволяет рассчитать в точности площадь сложных фигур и это достаточно просто, если понять что собой представляет геометрический смысл определенного интеграла. Данные расчеты можно рассмотреть наглядно на примере криволинейной трапеции. Связь между интегралом и параметром площадь фигуры определенно существует, остается только научиться распознавать ее и использовать для расчета площади.

Для начала следует понять, что такое криволинейная трапеция, ведь именно от ее площади нужно отталкиваться при вычислении. Криволинейная трапеция это нечто иное как плоская фигура, чьи границы определяются функцией непрерывного неотрицательного типа и двумя прямыми и осью абсцисс. Согласно этому понятию можно суммировать значения функции y = f(x) и таким образом определить площадь фигуры. Значения, которые необходимо суммировать, важно учитывать через бесконечно малые промежутки по оси между точками а и b, которые определяют границы фигуры. Такой подход к расчету площади позволяет разбивать целую фигуру на бесконечное количество прямоугольников, что упрощает расчет всей площади. У каждого прямоугольника есть длина и ширина согласно значению ординаты f(x) и оси Ох через бесконечно малые промежутки.

Формула расчета площади криволинейной трапеции

Геометрический смысл определенного интеграла определение

Геометрический смысл определенного интеграла в ином понимании это площадь криволинейной трапеции для неотрицательной и непрерывной функции, которая расположена между двумя интервалами. Так как криволинейную трапеции можно воспринимать как квадрируемую фигуру, то и подобный тип расчета площади является актуальным. Для того чтобы определенный интеграл мог существовать, очень важно, чтобы соблюдалось условие непрерывности функции.

Существует возможность определить, если заданная функция имеет определенный интеграл, но согласно общепринятой теореме в первую очередь рассматривается интегрируемость непрерывных функций. Изучение геометрического смысла определенного интеграла, как правило, всегда изучается в сочетание с определением площади для фигуры под названием криволинейная трапеция. Практическая польза данного понятия сводится к возможности расчета площади сложных фигур. Данные правила расчета актуальны для фигур с площадью в рамках линий x=g(y) и y=f(x).

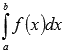
Все очень просто, достаточно вычислить интеграл и площадь сложной фигуры станет известной. Любую фигуру созданную из несколько линий по типу y = f(x), x = a, y = 0, x = b может вычисляться таким образом. Расчет возможен при условии, что функция не является положительной на отрезке между а и b, только принцип расчета частично отличается.

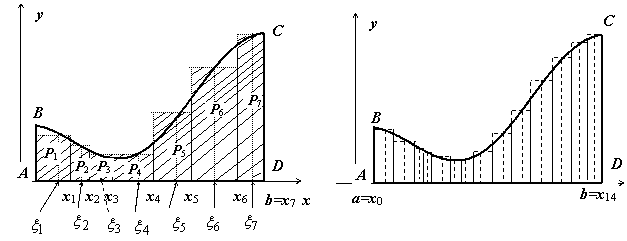
Обобщая вышесказанное можно заявить, что каждая сложная фигура является по факту криволинейной трапецией, а это значит, все вышеперечисленные расчеты актуальны для них. Успешный расчет площади сложных фигур возможен, если начинать с расчета более простых примеров и постепенно совершенствовать свои навыки. Согласно всему вышесказанному становится понятно, что геометрический смысл определенного интеграла позволяет решать одну из сложных задач геометрии – вычисление площади сложных фигур. Это становится возможным за счет применения интеграла, то, что одновременно и упрощает и усложняет задачу. В мире математики все понятия между собой тесно связаны и поэтому в обучении не должно быть пробелов, если вы стремитесь к определенным успехам.