Теорема Фалеса

Если стороны угла, пересекают прямые параллельные линии которые одну из сторон разделяют на несколько отрезков, то и вторую сторону, прямые так же разделят на равнозначны с другой стороной отрезки.

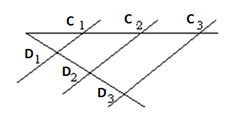
Теорему Фалеса доказывает следующее: С₁, С₂, С₃ — это места где пересекаются прямые параллельные на любой стороне угла. С₂ находится посередине относительно С₁ и С₃.. Точки D₁, D₂, D₃ — это места где пересекаются прямые, которые соответствуют прямым с другой стороной угла. Доказываем, что когда C₁C₂ = C₂C_з, значит и D₁D₂=D₂D₃.
Проводим в месте D₂ прямой отрезок КР, параллельный участку C₁C₃. В свойствах параллелограмма C₁C₂=KD₂, C₂C₃= D₂P. Если C₁C₂=C₂C₃, то и KD₂=D₂P.

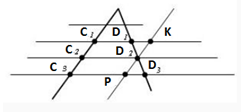
Полученные треугольные фигуры D₂D₁K и D₂D₃P равняются. И D₂K=D₂P по доказательству. Углы с верхней точкой D₂ равняются как вертикальные, а углы D₂KD₁ и D₂PD₃ равняются как внутренние накрест лежащие при параллельных C₁D₁и C₃D₃ и разделяющей KP.
Так как D₁D₂=D₂D₃ теорема доказана по равенству сторон треугольника

Заметка: Если взять не стороны угла, а два прямых отрезка, доказательство будет такое же.
Любые прямые отрезки параллельные друг другу, которые пересекают две рассматриваемые нами прямые и разделяющие одну из них на одинаковые участки, тоже самое делают и со второй.

Рассмотрим несколько примеров

Первый пример

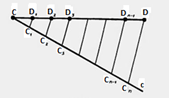
Условием задания требуется разбить прямую СD на п одинаковых отрезков.
Проводим от точки С полу-прямую с, которая не лежит на прямой СD. Отметим на ней одинаковые по величине части. СС₁, С₁С₂, С₂С₃ .....С_п-1С_п. Соединяем С_п с D. Проводим прямые от точек С₁,С₂,....,С_п-1 которые будут параллельны относительно С_пD. Прямые будут пересекать СD в местах D₁ D₂ D _п-1 и разделять прямую СD на п одинаковых отрезков.

Второй пример

На стороне АВ треугольника АВС отмечена точка СК. Отрезок СК пересекает медиану АМ треугольника в точке Р, при этом АК= АР. Требуется найти отношение ВК к РМ.
Проводим через точку М прямой отрезок, параллельный СК, который пересекает АВ в точке D

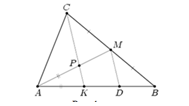
По теореме Фалеса ВD=КD
По теореме пропорциональных отрезков получаем, что
РМ = КD = ВК/2, следовательно, ВК : РМ = 2:1
Ответ: ВК: РМ = 2:1

Третий пример

В треугольнике АВС, сторона ВС = 8 см. Прямая DE пересекает стороны АВ и ВС параллельно АС. И отсекает на стороне ВС отрезок ЕС = 4см. Доказать, что АD = DВ.

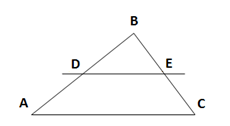
Так как ВС = 8 см и ЕС = 4см, то
ВЕ = ВС-ЕС, следовательно, ВЕ = 8-4 = 4(см)
По теореме Фалеса, так как АС параллельна DE и ЕС = ВЕ то, следовательно, АD = DВ. Что и требовалось доказать.

В женском журнале - онлайн, Вы найдете много интересной информации для себя. Так же есть раздел, посвященный стихам которые написал Сергей Есенин. Заходите не пожалеете!

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---