 Онлайн калькулятор
Онлайн калькулятор
 Решение матриц
Решение матриц
 Конвертор величин
Конвертор величин
 Решение кв. уравн.
Решение кв. уравн.
 Таблица Брадиса
Таблица Брадиса
 Тригоном. таблицы
Тригоном. таблицы
 Тесты и игры
Тесты и игры
 Решить задачу
Решить задачу
 Таблица производных
Таблица производных
 Калькулятор дробей
Калькулятор дробей
 Фонетический разбор
Фонетический разбор
 Редактор формул
Редактор формул
Теорема Пифагора доказательство
Обращаясь к истории, теорема Пифагора хоть и носит название Пифагора, но открыл ее не он. Так как особые свойства прямоугольного прямоугольника ученые начали изучать намного раньше его. Тем не менее есть два утверждения. Первое гласит о том что Пифагор доказал теорему. Второе, соответственно что не он. На данным момент не проверить какое из этих мнений верно, но к сожалению, если и было доказательство Пифагора, то оно не дожило до нашего времени. Так же есть мнение что доказательство сделанное Евклидом, было сделано Пифагором, а Евклид его обнародовал.
Несомненно в Египте во времена правления фараонов, возникали вопросы с прямоугольным треугольником. В истории Вавилона он так же участвовал. Из чего можно сделать вывод, что данная теорема, вызывала интерес с древних времен. На сегодняшний день существует 367 различных доказательств. Чем не может похвастать ни какая другая теорема.
Заметка: Если Вы ищите мебель для лаборатории или просто хотите приобрести вытяжной шкаф (http://www.labmet.ru/shkafy-vytyazhnye.html). Перейдите по данной ссылке и купите все что нужно. Качество гарантированно!
Разберем основные доказательства.
1 Теорема Пифагора доказательство.
Считается что это легкий способ. В нем применяются правильные треугольники.

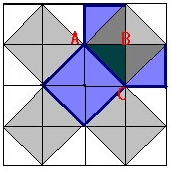
если взять равнобедренный прямоугольный треугольник АВС, от гипотенузы АС мы сможем построить квадрат, в котором находятся 4 аналогичных треугольника. С помощью катета АВ и ВС строятся квадраты, содержащие в себе еще по два таких же треугольника.
2 Теорема Пифагора доказательство.
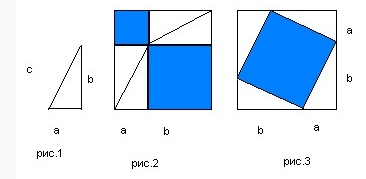
Здесь сочетается как алгебра так и геометрия. Изображаем прямоугольный треугольник abc. И 2 квадрата равных двум длинам катетов а+b. Затем сделаем построение, как на рисунках 2, 3. Вследствие чего получим два квадрата со сторонами а и b. Второй квадрат содержит 4 треугольника, образуя таким образом квадрат равный гипотенузе c. Интересно что общая площадь квадратов на рис. 2, 3 равная друг другу.
Обобщая все в формулу мы получим. а2+b2 = (а+b)2 - 4 * 1/2 * а * b. Раскрыв скобки получим а2+b2= а2+b2. Площадь рис.3 вычисляем как S=c2 или а2+b2=с2.ч.т.д.
3 Теорема Пифагора доказательство.
Доказательство найдено в 12 вв, в древней индии.
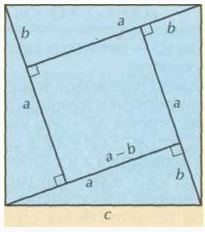
Построим в квадрате 4 треугольника (прямоугольных). Гипотенузой будет сторона с, катетами в треугольнике а и b. Вычисляем площади квадратов большой- S=c2, и внутренний
(а-b)2 2 +4 * 1/2 * а * b. Из чего вывод, что с2= (а-b)2 2+ 4 * 1/2 * а * b, а следовательно, с2= а2+b2.
4 Теорема Пифагора доказательство.
Основано на геометрии, носит название Метод Гарфилда. Построением прямоугольного треугольника ABC найдем доказательство тому , что BC2=AC2+AB2.Продолжим катет AC, создав прямую СD равную катету AB. Соединяя прямую и угол E перпендикулярно АD получаем ED. Прямые AC и ЕD равные между собой.
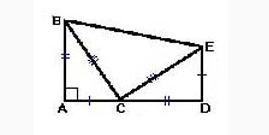
Для доказательства данного действия, воспользуемся так же двумя методами, приравнивая этим выражения.
Находим площадь многоугольника АВЕD. Так как АВ=СD, АС=ЕD, ВС=СЕ, значит SАВED= 2*1/2 (АВ*АС)+ 1/2 ВС2.
Мы видим что АВСD трапеция. А значит SАВСD = (DE+AB)*1/2AD.
Представим эти методы вместе приравнивая их:
AB*AC+ 1/2 BC2= (DE+AB)*1/2(АС+CD).
Упростим АВ*АС +1/2ВС2= 1/2(АВ+АС)2.
Раскрыв скобки получаем : АВ*АС+1/2ВС2=1/2АС+2*1/2(АВ*АС)+1/2АВ2.
Итог: ВС2=АС2+АВ2. ч.т.д.
Это далеко не все способы доказательства теоремы Пифагора, но основные из них.
- Блог пользователя kak-reshit
- Войдите на сайт для отправки комментариев


 Образовательный портал
Образовательный портал Reshit.ru может исчезнуть — нужна ваша поддержка!
Reshit.ru может исчезнуть — нужна ваша поддержка!
Пифагоровы штаны известны даже малышам, которые и не понимают вовсе о чем речь то идет. На мой взгляд это самая легкая теорема. Мне повезло что именно она попалась в билетах)))
Интересно было бы все эти 367 доказательств в кучу собрать, целая книга бы вышла.
Ух ты! Впервые слышу, что теорему Пифагора на самом деле придумал, вернее вывел эту теорему не он. А кто же тогда на самом деле у нас должен столько лет быть в почете?!