 Онлайн калькулятор
Онлайн калькулятор
 Решение матриц
Решение матриц
 Конвертор величин
Конвертор величин
 Решение кв. уравн.
Решение кв. уравн.
 Таблица Брадиса
Таблица Брадиса
 Тригоном. таблицы
Тригоном. таблицы
 Тесты и игры
Тесты и игры
 Решить задачу
Решить задачу
 Таблица производных
Таблица производных
 Калькулятор дробей
Калькулятор дробей
 Фонетический разбор
Фонетический разбор
 Редактор формул
Редактор формул
Второй закон Кирхгофа
Законы Кирхгофа являются важной частью электротехники, их можно использовать для теоретических расчетов и с практической пользой в случае электрических цепях разветвленного и произвольного типа. Первый закон и второй закон Кирхгофа пользуются особым спросом благодаря своего универсального применения и возможности решить различного рода задач. Они работают, так как для линейных цепей, так и для нелинейных, где ток может быть переменным или постоянным. В некоторых источниках законы Киргофа принято называть правилами, так как выводы были сделаны на основе длительного наблюдения за определенными процессами.
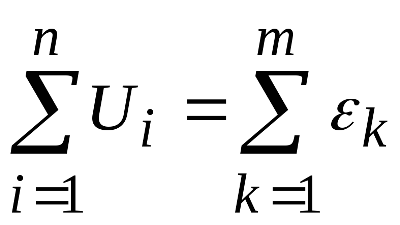
До того как понять, что собой представляет второй закон Кирхгофа стоит вспомнить, что именно гласит первый закон, так как между ними определенно должна быть какая-то связь, учитывая, в том числе последовательность их появления. Несмотря на то какая формулировка, первый закон Кирхгофа гласит одну истину:
Первая формулировка : Сумма всех токов, которые сводятся в один узел, равна нулю.
Вторая формулировка: Сумма тех токов, которые являются втекающими и вытекающими из единого узла представляет собой одно и то же значение, то есть эти два значения равны.
Речь именно об алгебраической сумме этих токов. Данный закон появился как производное от закона сохранения заряда. Другими словами первый закон указывает на непрерывность тока. Первый закон может быть сформулирован по-разному, но вне зависимости от этого он будет означать то же самое понятие. Если первый закон гласит, что сумма всех токов входящие в один узел равна сумме всех токов выходящих из этого узла, то не составит труда сформулировать на основе этого и второе неопровержимое правило Кирхгофа.
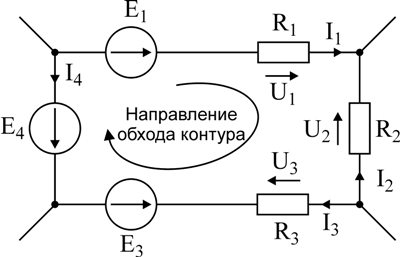
Понимание правил Кирхгофа можно упростить, если удостовериться, что такие простые понятия как ветвь, узел, контур и электрическая цепь являются понятными и доступными. Разъяснение можно начать с самого простого понятия – ветвь, что представляет собой некую часть электрической цепи с одинаковым током по всей длине. Узел более сложное понятие, так как он может состоять из определенного количества ветвей, которые объединены в одной точке. Понятие контур уже некий замкнутый электрический путь, который может состоять из разного количества ветвей и узлов. Путь обязательно закрытый и подразумевает возврат в исходную точку после прохождения всех элементов электрической цепи. Несколько контуров могут существовать бок о бок и делить между собой свои элементы, так как ветви и узлы. Все эти значения обозначают второй закон Кирхгофа.
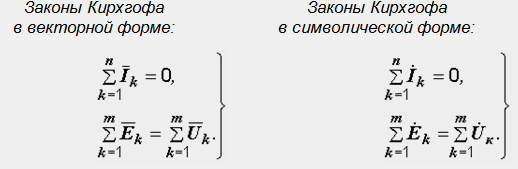
Второй закон Кирхгофа и его определение
В едином замкнутом контуре алгебраическая сумма ЭДС будет равняться на значение, которое суммирует изменения напряжения на всеобщее количество резистивных элементов данного контура.
Второе правило Кирхгофа актуально в сетях с постоянным и/или переменным током. В формулировке закона используется именно понятие алгебраическая сумма, так как она может быть указана со знаком плюс или минус. Точное определение возможно в таком случае только посредством простого, но эффективного алгоритма. Для начала надо подобрать какое-то направление для обхода контура, по/против часовой стрелке, на собственное усмотрение. Само направление тока подбирается только через элементы цепи. После следует определить знаки «+» и «-» для напряжениях и ЭДС. Напряжения нужно записывать с отрицательным знаком, когда ток не соответствует обходу контура в плане направления и с плюсом в случае совпадения. То же самое правило нужно использовать и в том случае, когда необходимо отметить ЭДС.
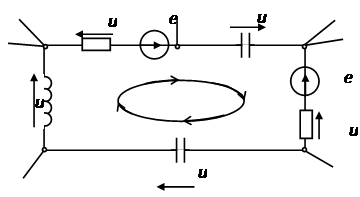
Второй закон Кирхгофа - практическое применение
На практике второй закон Кирхгофа применяется успешно для расчета электрических цепей. Благодаря его разъяснению можно рассчитать необходимые параметры в сложных электрических цепях. Когда присутствует необходимость рассчитать значение тока и/или направление всегда выручит второй закон Кирхгофа. Невзирая на то, что правила Кирхгофа были сформулированы в далеком 1845 году, они показали себя как рабочие и не вызывают вопросы ни у кого. Теория электрических цепей была бы неполной без наличия этих законов, которые так хорошо подходят для решения различных уравнений в этой области.
- Блог пользователя zakony
- Войдите на сайт для отправки комментариев


 Образовательный портал
Образовательный портал Reshit.ru может исчезнуть — нужна ваша поддержка!
Reshit.ru может исчезнуть — нужна ваша поддержка!