 Онлайн калькулятор
Онлайн калькулятор
 Решение матриц
Решение матриц
 Конвертор величин
Конвертор величин
 Решение кв. уравн.
Решение кв. уравн.
 Таблица Брадиса
Таблица Брадиса
 Тригоном. таблицы
Тригоном. таблицы
 Тесты и игры
Тесты и игры
 Решить задачу
Решить задачу
 Таблица производных
Таблица производных
 Калькулятор дробей
Калькулятор дробей
 Фонетический разбор
Фонетический разбор
 Редактор формул
Редактор формул
Как находить периметр треугольника
В статье на примерах покажем, как находить периметр треугольника. Рассмотрим все основные случая, как найти периметры треугольников, даже когда не все значения сторон известны.
Треугольником называется простая геометрическая фигура состоящая из трех прямых линий пересекающих друг друга. В которой точки пересечения прямых, называются вершинами, а прямые линии соединяющие их, называются сторонами.
Периметром треугольника называется сумма длин сторон треугольника. От того сколько мы имеем изначальных данных, для вычисления периметра треугольника, зависит каким из вариантов мы воспользуемся, для его вычисления.
Первый вариант
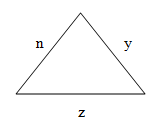
Если мы знаем длины сторон n, y и z треугольника, то периметр мы можем определить с помощью следующей формулы: в которой P - это периметр, n, y, z- стороны треугольника
 периметр прямоугольника формула
периметр прямоугольника формула
P = n + y + z
Рассмотрим на примере:
Дан треугольник ksv стороны которого k = 10см, s = 10 см, v =8см. найти его периметр.
Пользуясь формулой получаем 10 + 10 + 8 = 28.
Ответ: Р = 28см.
Для равностороннего треугольника находим периметр так - длина одной стороны умноженная на три. формула выглядит следующим образом :
Р = 3n
Рассмотрим на примере:
Дан треугольник ksv стороны которого k = 10см, s = 10 см, v =10см. найти его периметр.
Пользуясь формулой получаем 10 * 3 = 30
Ответ: Р = 30см.
Для равнобедренного треугольника находим периметр так - к длине одной боковой стороны умноженной на два, прибавляем сторону основания
Равнобедренным треугольником называется простейший многоугольник у которого две боковые стороны равны, а третья сторона называется основанием.
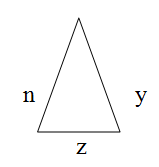
P = 2n + z
Рассмотрим на примере:
Пользуясь формулой получаем 2 * 10 + 7 = 27.
Ответ: Р = 27см.
Второй вариант
Когда нам не известна длина одной стороны, но мы знаем величины длины двух других сторон и угла между ними, а периметр треугольника возможно найти только после того как мы узнаем длину третьей стороны. В этом случае неизвестная сторона будет равна корню квадратному из выражения в2 + с2 - 2 ∙ в ∙ с ∙ cosβ
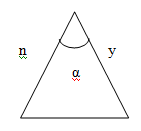
P = n + y + √ ( n2 + y2 - 2 ∙ n ∙ y ∙ cos α )
n, y - длины сторон
α - размер угла между известными нам сторонами
Третий вариант
Когда нам не известны стороны n и y, но мы знаем длину стороны z и величины прилегающих к ней. Периметр треугольника в этом случае мы сможем найти только тогда когда узнаем длины двух неизвестных нам сторон, определим их с помощью теоремы синусов, с помощью формулы
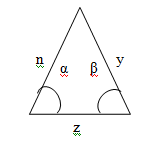
P = z + sinα ∙ z / (sin ( 180°-α - β )) + sinβ ∙ z / (sin ( 180°-α - β ))
z - длина известной нам стороны
α, β - размеры известных нам углов
Четвертый вариант
Так же можно найти периметр треугольника по радиусу вписанному в его окружность и площади треугольника. Определяем периметр по формуле
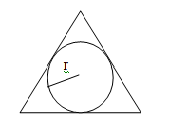
P = 2S / r
S - площадь треугольника
r - радиус вписанной в него окружности
Мы с вами разобрали четыре разных варианта, как можно найти периметр треугольника.
Находить периметр треугольника в принципе не сложно. Если у вас появились какие то вопросы по статье, дополнения, то обязательно пишите их в комментариях.
Кстати, на referatplus.ru вы можете скачать рефераты по математике бесплатно.
- Блог пользователя admin
- Войдите на сайт для отправки комментариев


 Образовательный портал
Образовательный портал Reshit.ru может исчезнуть — нужна ваша поддержка!
Reshit.ru может исчезнуть — нужна ваша поддержка!
Как найти периметр треугольника я в принципе знала и не раз этой формулой пользовалась, но чтобы по радиусу вписанной окружности - даже не догадывалась что такое бывает.
Я пару раз пыталась по радиусу и ничего у меня не получилось, скорее всего что то не так мерила. Я вручную пробовала, не в задачке в смысле.
Не вижу разницы, нарисованы то все равнобедренные треугольники, не путайте нас!
Смешная статья конечно, разве у кого нибудь бывают проблемы с вычислением периметра треугольника?! Мне кажется что это самая легкая геометрическая фигура.