Рассказываем чему равна и как рассчитать площадь круга.

Площадь круга

Площадь круга равна произведению константы π на квадрат радиуса измеряемой нами окружности. В виде формулы это утверждение можно представить следующим образом:

Sокр= πr², где

π – константа. Она определяется делением длины окружности на диаметр(ширину) фигуры;

r – радиус окружности.

Известно, что площадь правильного многоугольника(правильный - значит все стороны равны) равна произведению апофемы (перпендикуляра опущенного на сторону из центра) на половину периметра фигуры. В свою очередь площадь многоугольника, количество сторон которого стремится к бесконечности, естественно стремится к площади окружности, в который этот многоугольник можно вписать. Так доказывается утверждение о том, что Sокр= πr².

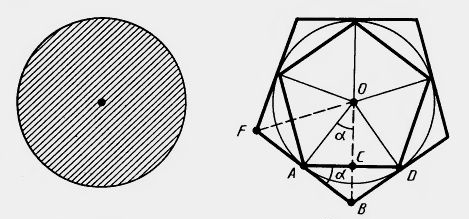
Площадь сегмента круга

Также во время решения различных задач может возникнуть необходимость рассчитать площадь сегмента круга. В этом случае нам необходимо знать угол сегмента. В этом случае расчет площади сегмента будет производиться по следующей формуле:

Sсег= Sокр*U/360, где

U – угол сегмента;

Sокр – площадь окружности.

Также площадь сектора круга может определяться по альтернативной формуле:

Sсег= ar²/2, где

a – угол сегмента, измеренный в радианах

Окунаясь в историю площади круга

В наши дни математиками может быть произведен расчет площади круга альтернативными методами, , например метод интегрирования, вещественного анализа и другие. Интересен тот факт, что древние математики также занимались определением этой величины. Зависимость площадей окружностей от их радиусов в квадрате была замечена еще в Древней Греции ученым Евдоксом Книдским. Теперь же и вы имеете представление о том, как рассчитать площадь круга, зная его радиус.

Также изучением вопроса определения площади круга занимался небезызвестный Архимед. Его метод определения формулы площади круга основывался на методах геометрии Евклида. Архимед доказал, что площадь треугольника с основанием, равным длине окружности и площадь круга - равны. По формуле длина окружности 2πr, площадь треугольника будет равна 2πrH/2, где H – высота треугольника, которая равная радиусу.

Если перед вами стала задача определить площадь круга или его отдельного сектора-сегметра – вы это легко сделаете, используя вышеприведенные формулы. Более подробно узнать о разных методах доказательства определения площади круга можно найти в справочной литературе.

Кстати РАБОТА (http://ewrazia.su) проекта ewrazia.su заключается в лизинге персонала по многим городам России и Европы.