Формула корней квадратного уравнения

формула корней квадратного уравнения

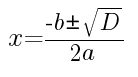
По приведенной выше формуле находятся корни квадратного уравнения в случаях, когда дискриминант больше нуля. Формула дискриминанта записывается, как D=b2- 4ac. 


В случае, когда дискриминант равен нулю уравнение имеет один корень, который находиться по формуле x = -b/2a.

Когда дискриминант меньше нуля, тогда чаще говорят о том, что у такого уравнения нет корней. Если точнее, то у уравнения дискриминант которого меньше нуля нет вещественных корней, однако существует 2 комплексных корня.

Еще формулы из базы:

объема, серная кислота, объем цилиндра, Пика, уксусная кислота, этанол, арифметическая прогрессия, сопротивление, скорости, длина окружности, тригонометрические, тригонометрии, разности квадратов, площади квадрата, работы, приведения, мела, площади трапеции, площади, дискриминанта, сила тока
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях: