Формула дискриминанта

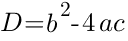
Дискриминант квадратного уравнения используется для упрощениях нахождения его корней.
Для уравнения общего вида ax²+bx+c=0 формула дискриминанта D = b²-4ac.
Отработать нахождение корней квадратного уравнения с использованием дискриминанта на практике можно, используя наш сервис.

Примеры нахождения дискриминанта по формуле.

Для уравнения.
x² + 3x + 2= 0
a=1 b=3 c=2
D = b²-4ac = 3² - 4*2*1= 9 -8 = 1

Для уравнения.
3x² - 7x - 1= 0
D = (-7)² - 4*(-1)*3= 49+12 = 61

Для уравнения.
2x² + x + 9= 0
D = 1² - 4*2*9= 1-72 = -71
Данной уравнение имеет комплексные корни, так как дискриминант меньше нуля.
Больше информации о решении квадратных уравнении в сервисе!

Еще формулы из базы:

длина окружности, мощности, плотности, спирта, соли, Герона, логарифмов, скорости, этиловый спирт, площади треугольника, понижения степени, напряженности, кислот, куба суммы, аммиак, оксида, щелочей, квадратного уравнения, соляная кислота, сопротивление, сокращенного умножения, угольная кислота, ЭДС, общая формула алкенов, объем призмы, энергия фотона, углекислый газ, средняя скорость, тангенса, магнитный поток, массы, емкость конденсатора

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---