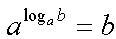Онлайн калькулятор
Решение матриц
Конвертор величин
Решение кв. уравн.
Таблица Брадиса
Тригоном. таблицы
Тесты и игры
Решить задачу
Таблица производных
Калькулятор дробей
Фонетический разбор
Редактор формул
Образовательный порталПоследнее в образовательном блоге
- Проверяемые безударные гласные в корне слова: примеры!
- Теории происхождения человека
- Как быстро выучить стих: эффективные методы
- Самостоятельные части речи, что это?!
- Пунктуационный разбор предложения: что это, основные правила и примеры
- От какого слова происходит слово "АРИФМЕТИКА" и её значение!
- Что изучает физика? Понятно о том, зачем учить физику!
- Таблица степеней с инструкцией
- Переход на дистанционное обучение. Рекомендации!
- Высшее образование дистанционно. База для обучения!
Логарифмические неравенства. Помогите решить.
Логарифмические неравенства. Помогите решить.
Кто понимает тему - логарифмические неравенства? Помогите решить. Признаюсь честно, я решать не пробовала, просто не знаю, как это делается.
log (2x+59) > -2
1/3
Помочь можем, но готовых решений не даем. Сначала нужно найти область допустимых значений, а потом, для решения именно этого неравенства, нужно использовать формулу
при 0 < а <1
log f(x) > b f(x) < a^b
а
А мы не так решали. Значение, стоящее в правой части неравенства, т.е. -2, подводим под знак log. И тогда уже решаем неравенство.
-2 = log 9
log (2x+59) > log 9, логарифмы с основанием1/3
А потом, с учетом того, что 0<а <1, можно записать 2x+59 < 9
Область допустимых значений находим из выражения (2x+59) >0
Нужно решить систему из двух уравнений
2x+59 > 0 --> x > -29,5
2x+59 < 9 --> x < -25
Ответ: -29,5< х < -25
Мы нашли промежуток значений х, на котором будет выполняться заданное неравенство.
Чтобы решать логарифмические неравенства и уравнения, нужно знать основные логарифмические свойства. В этом примере было использовано следующее свойство:
Отправить комментарий