Как рассчитать периметр

сб., 2015-05-23 12:16 — avokat

Народ, как рассчитать периметр правильного шестиугольника вписанного в окружность, если известен только радиус окружности? Нужны подсказки, советы, решение. Всё, всё, и всего побольше)))))

сб., 2015-05-23 14:04 — belost

Смотрите, я нашел чертеж соответствующий вашей задаче. Если мы проведем в окружности диаметры, соединяющие вершины шестиугольника, то получим, шесть одинаковых равнобедренных треугольников, у которых радиусы окружности являются боковыми сторонами. Рассмотрим один из них. Из вершины О, треугольника АОВ, можно провести высоту, которая разделит сторону АВ на 2 равные части. Найдем длину одной из частей (элементарно), а далее вычислим периметр.
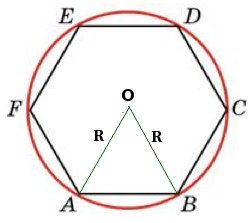
периметр

вс., 2015-05-24 15:01 — avokat

Возможно, что для вас элементарно, но я до сих пор не пойму, что нужно делать. В условии дан только радиус окружности. Была бы известна высота, я применил бы теорему Пифагора, и нашел половину стороны отрезка АВ. Не вижу, что делать дальше. Нужны еще подсказки.

пн., 2015-05-25 15:09 — Зайя

Сначала нужно найти угол АОВ.
360/6 = 60 градусов
далее, можно вычислить углы при основании треугольника (они будут равны)
(180-60)/2 =60
А теперь осталось применить формулу косинуса для острых углов в прямоугольном треугольнике
cosОАВ = 1/2|АВ| / |ОА|

ср., 2015-05-27 19:00 — Alenka

Ну, вы тут уже все разжевали))) осталось внести последнюю каплю
|АО| = |ОВ| = |АВ| = R
Вы что, не заметили, что все углы в треугольнике равны 60 градусов! А следовательно, он равносторонний, а не равнобедренный.

ср., 2015-05-27 19:32 — Изюмина

Я за вариант решения, который предложила Аленка